Vectors and Kinematics (Part 1 of 2)
You can find the second part of this series here: Vectors and Kinematics (Part 2 of 2).
Vectors and Scalars
- A vector is a quantity that has magnitude (size) and direction. For example:
- Velocity, displacement, acceleration
- A scalar is a quantity that has only magnitude (size). For example:
- Speed, distances, temperatures, mass
5 miles per hour = scalar quantity
5 miles per hour, east = vector quantity
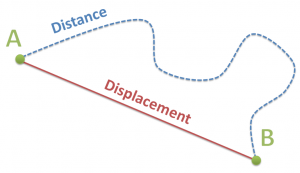
Displacement
Displacement is the change in position of an object. This is not the total distance an object has travelled.
The total distance travelled can be greater than the magnitude of its displacement.
- A’s Displacement = Δx = xfinish – xstart = e.g. 10 meters
- Distance = total length of distance travelled, for the sake of the example, 20 meters
Velocity
Velocity is a vector quantity. It is speed, and direction. Instantaneous velocity is the speed and direction at a certain point in time.
Acceleration
Acceleration is the change in velocity over time. It is also a vector quantity.
For example: 0 – 60 miles per hour, in 3 seconds east
- a = Δv / Δt
- 60 – 0 (east) / 3 seconds = 20 miles per hour/seconds (east)
Linear Motion
Linear motion = change in distance / change in time.
Question: A ball thrown straight up in the air at 20 meters / second
- How long will the ball move up?
- How high will the ball travel?
Gravity = 9.8 meters / second2 ⇒ velocity due to gravity = g × t
Distance = v × t
Distance due to gravity = ½ g t2
Answer Part 1:
Initial velocity = 20 m/s
∴ 20 m/s = 10 m/s2 t ← gravity approximation (9.8 to 10)
∴ t = 2 seconds
Part 2:
20 m/s × 2 – ½ (10 m/s2)(2)2
40 m – 20 m
= 20 meters, before it starts to descend





You must be logged in to post a comment.